Significant figures relate to numbers, so learning about them through words may seem a bit confusing at first. It is important to look at the examples towards the bottom if you are confused by any rules.
What are Significant Figures
Significant figures indicate how accurate a value or measurement is. The more significant figures a number has, the more accurate it is. It is important to understand them because they determine what place you should round to in problems that involve calculations.
Determining Number of Sig Figs
1. All nonzero digits are significant.
2. All leading zeros are not significant. Leading zeros occur before any nonzero digits, like the bolded zeros in 0.0003240
3. All zeros after a nonzero digit are significant, unless they are trailing zeros (explained below).
4. Trailing zeros are not significant unless there is a decimal point. Trailing zeros are before the decimal point but after the last nonzero digit. For example the bolded zeros in 3000, 99800, and 10100 are trailing, meaning they are not significant. The zeros in 58009 are not trailing because there is a 9 after them. The zeros in 3000.0 are not trailing because there is a decimal point.
Operation Rules
When you do calculations, this is how you round your answer to the appropriate amount of sig figs.
Multiplication/Division: When multiplying or dividing numbers, look at which number has the least amount of sig figs. The answer should have the same amount.
Addition/Subtraction: Find the number with the least amount of decimal places. Your answer should have the same amount of decimal places.
Measurement Rules
When looking at a ruler, volumetric flask, or any type of visual measurement, this is how you determine the sig figs of your measurement.
Look at the smallest provided increment, and add one estimated digit.
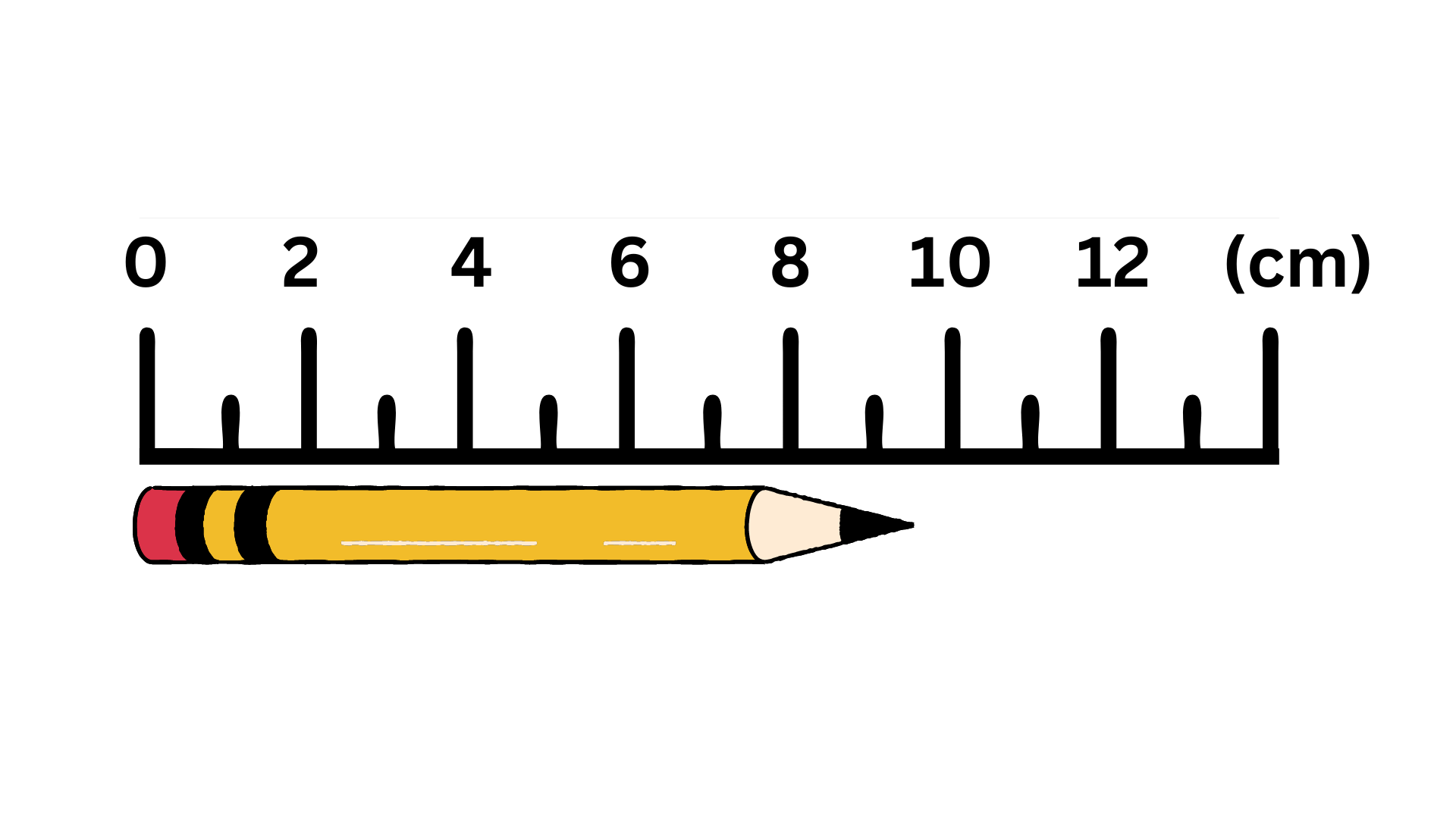
The smallest increment on the ruler is 1 cm. So we can measure to the centimeter and one more estimated digit (tenth of a centimeter). It is definitely between the 9 and 10 cm mark. We can estimate that it is about 9.5 cm. We cannot estimate any further past the tenth of a centimeter.
Examples
Note that the bolded digits are significant.
0.0034 has two sig figs. The zeros are not significant because they come before any nonzero digits.
1.0034 has 5 sig figs. Now, the zeros are significant because they come after a 1.
1.00340 has 6 sig figs. That last zero is not a trailing zero because there is a decimal point, so it is significant.
10300 has 3 sig figs. The last two zeros are trailing.
10300. has 5 sig figs. The last zeros are no longer trailing because there is a decimal point.
103004 has 6 sig figs. Again, these zeros are not trailing because there is a 4 after them.
12.64 x 14.3 = 181 The number with the least sig figs is 14.3, with three sig figs. So the answer, 181, is rounded to three sig figs.
100 x 301.765 = 30000 The number 100 only has one sig fig. The answer, 30000, is rounded to one sig fig.
0.00524 / 4.578 = 0.00114 The number 0.00524 has the least sig figs (three), so the answer is rounded to three sig figs.
101 x 14 / 654.2 = 2.2 The number with the least sig figs is 14 (two sig figs), so the answer is rounded to two sig figs.
10.545 + 1.2 = 11.7 For addition, we only look at digits after the decimal. 1.2 has one digit after the decimal, so we round 11.7 to one digit after the decimal.
9999.456 – 12.3441 = 9987.112 For subtraction, we also look at digits after the decimal. 9999.456 has the least digits after (three digits), so we round the answer to three digits after the decimal.
