Velocities
These velocity equations all include R (the ideal gas constant), T (temperature), and M (molar mass). For these equations, R = 8.314 J/(mol • K), temperature should be in Kelvin, and molar mass should be in (kg/mol).
Average Velocity: The mean velocity of all of the molecules in a gas. If you were to measure the velocity of each particle, and then average those velocities, you would find the average velocity. However, it would be extremely difficult to measure the velocity of each individual molecule, so instead we can use the following equation ↴

Most Probable Velocity: The velocity held by the greatest fraction of molecules in a gas. If you were to measure the velocity of all of the molecules in a gas, this would be the mode (the most frequently appearing velocity). The most probable velocity can be found using the following equation ↴

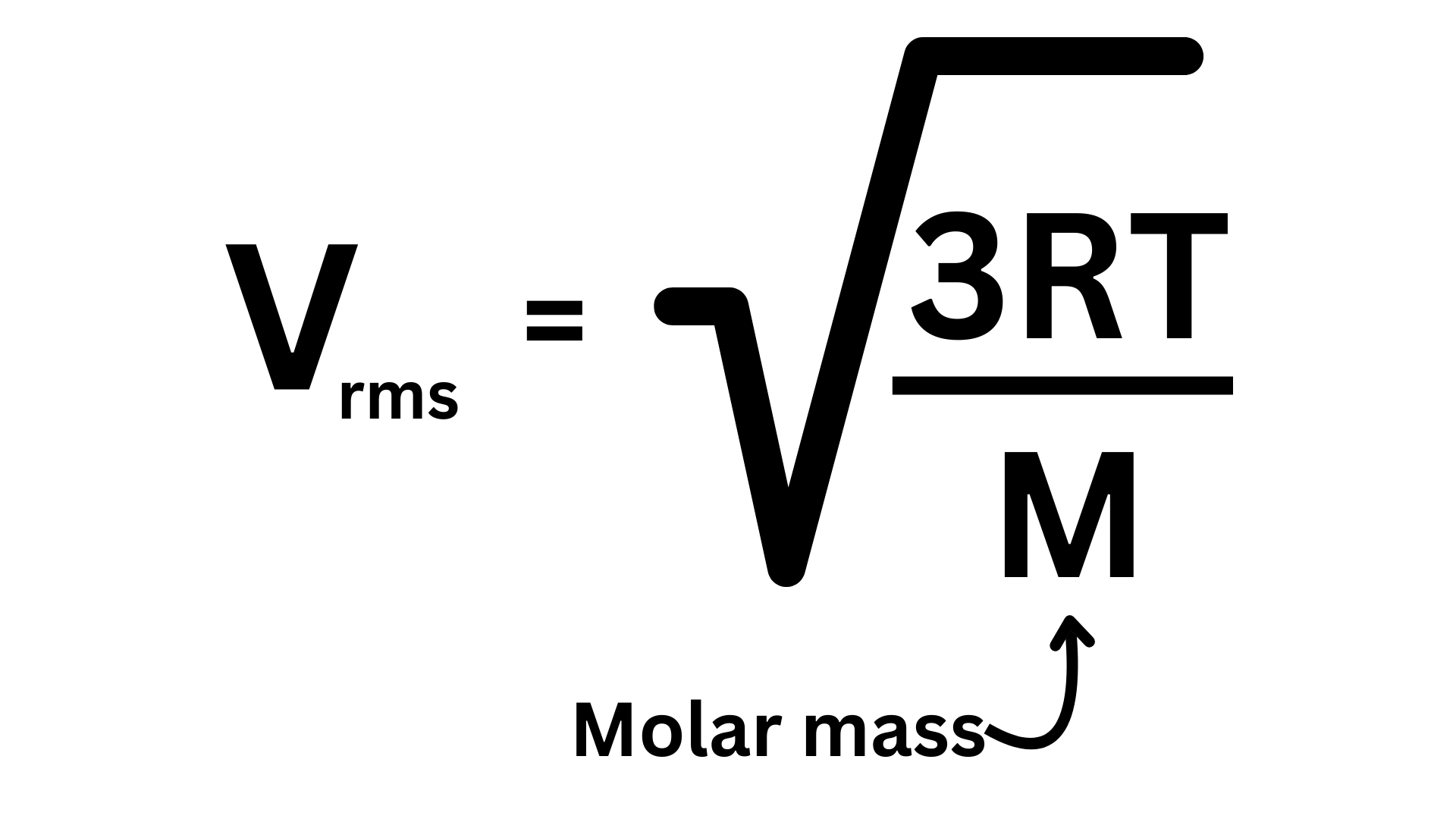
Root Mean Square Velocity: The velocity of a gas molecule that has average kinetic energy. If you were to measure the kinetic energy of each particle in a gas, and then find the average KE, a molecule with that average KE possesses the root mean square velocity. This may seem similar to average velocity. For the average velocity, we simply are finding the mean velocity. For the root mean square velocity, we are finding the mean KE, and then looking at the velocity of a particle with the mean KE. In the kinetic energy equation, KE = ½ mv², velocity is squared, which is why the root mean square velocity does not equal the average velocity. In fact, the root mean square velocity will always be slightly greater. Here is how you find the root mean square velocity ↴
Now, let’s do an example finding all three ↴
Example Problem
Calculate the most probable, average, and root mean square velocity of carbon dioxide at 60.0 ˚C
Answer

Maxwell Distribution Curve
Recall that temperature is proportional to the average kinetic energy of a gas. This does not mean that all particles in the gas have the same kinetic energy. In fact, the molecules in a gas are traveling at many different speeds. The Maxwell Distribution Curve allows us to look at the distribution of these speeds.
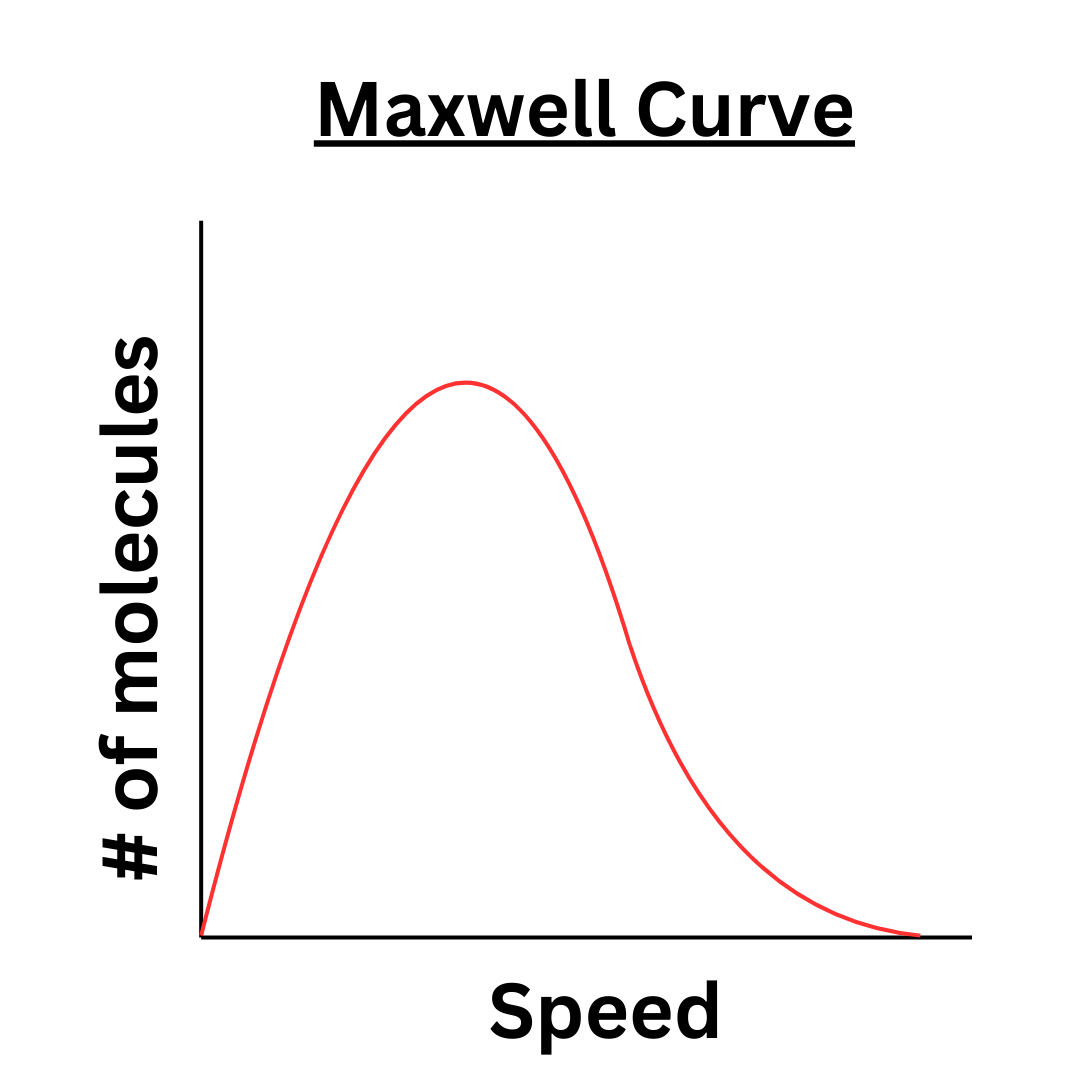
The x-axis represents the speed of the gas molecules. The y-axis represents the number of particles at that speed.
We can also point out the average, most probable, and root mean square velocities on a Maxwell Curve.

As you can see, the most probable velocity is the highest point on the curve, meaning that it is the velocity held by the greatest number of molecules.
Also note how the root mean square velocity is slightly greater than the average velocity. You will not have to be able to identify these two on a Maxwell Curve. However, you should be able to identify the most probable velocity with ease.
Comparing Maxwell Distribution Curves
How does the Maxwell Curve change as the temperature changes? As temperature increases, the kinetic energy of the gas particles increases. Therefore, the velocities of the particles increase. This creates the following effect ↴
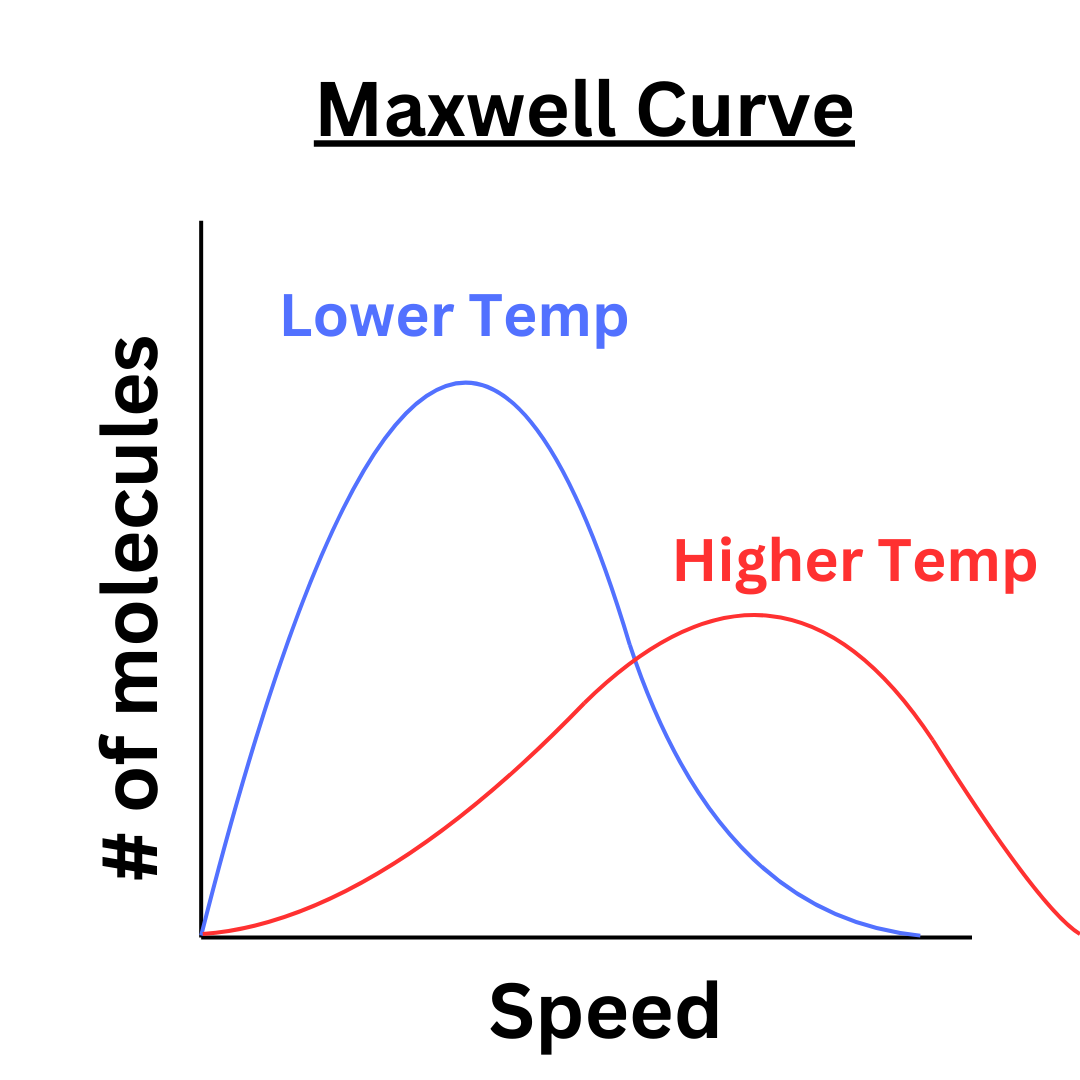
As temperature increases, the curve flattens out and shifts right. As explained above, an increase in temperature causes an increase in the speeds of the molecules. However, the number of particles doesn’t change. So as the range of velocities expands, there is a wider distribution of gas molecules, causing the curve to flatten.
Now that we’ve compared different temperatures, let’s compare different gasses at the same temperature. When two gasses are at the same temperature, they have the same average kinetic energy. KE = ½ mv², so the gas with the greater mass will have slower molecules. The lighter gas will have faster particles.
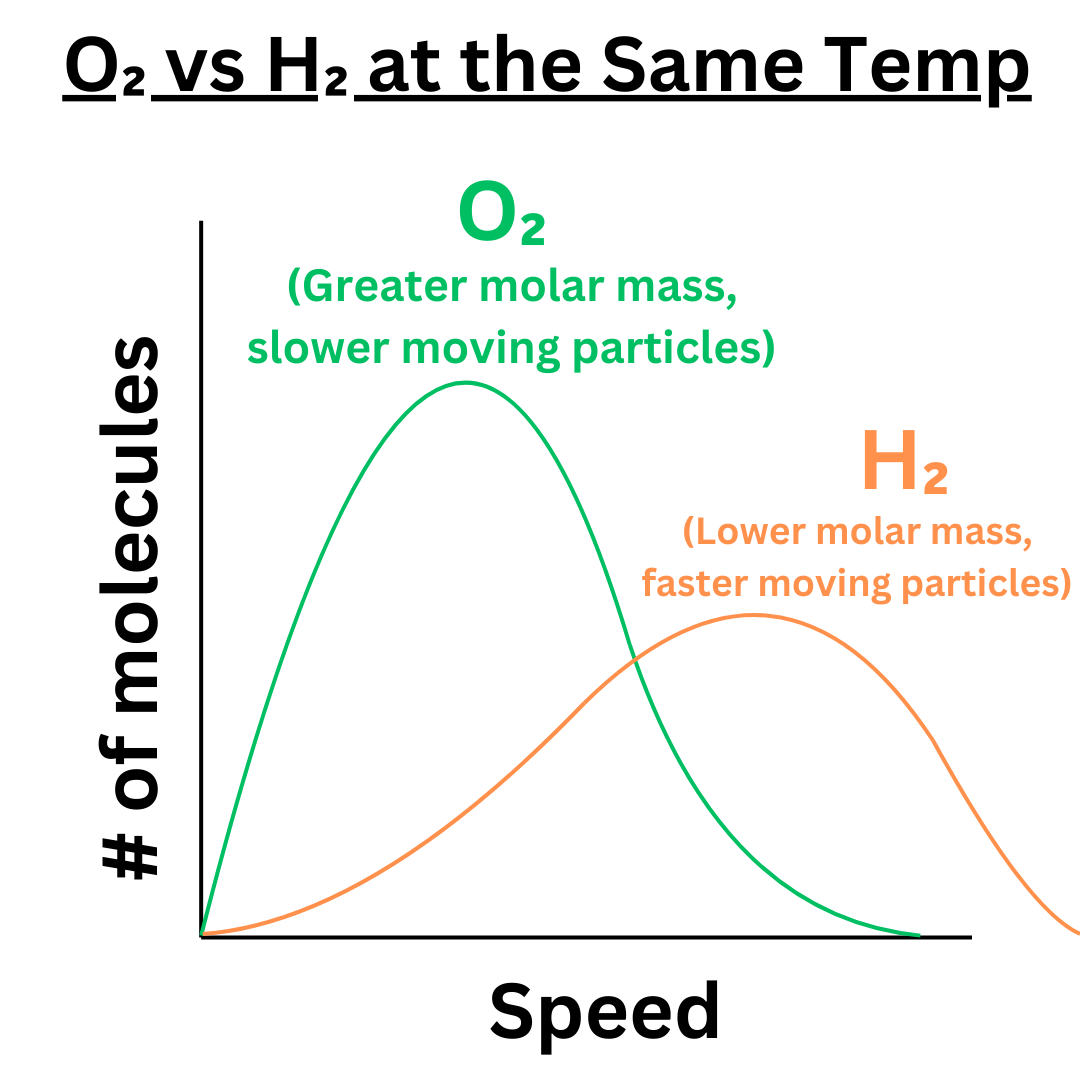
As you can see, the lighter gas has a curve that is flattened and shifted right compared to the heavier gas. This is similar to the effect of changing temperature.
